Dynamic FBA

Dynamic flux balance analysis (DFBA) enables the simulation of dynamic biological systems by assuming that organisms reach a steady state rapidly in response to changes in the extracellular environment [Mahadevan et al., 2002]. The fluxes predicted by FBA are then used to update the extracellular environment. Because simulations can now incorporate time-dependent changes, DFBA can provide temporal profiles of nutrient consumption, product formation, and biomass accumulation in the microbial community.

For example, dynamic model predictions for anaerobic batch growth of wild-type E. coli on glucose/xylose media are shown below [Hanly and Henson, 2011].

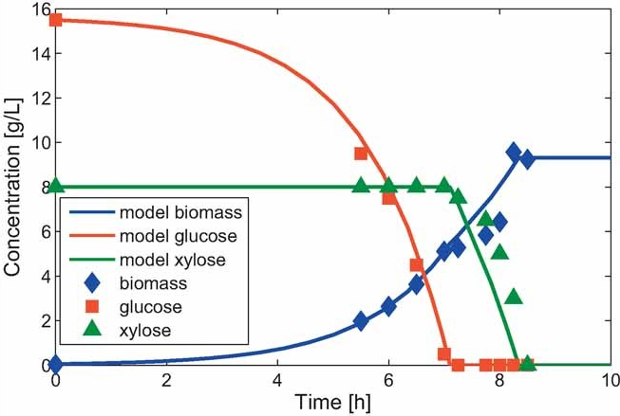
Fig. 5 Comparison of DFBALab model predictions and experimental data [Eiteman et al., 2008] for wild-type E. coli aerobically consuming a mixture of glucose and xylose.

Environment Setup

For performing comprehensive constraint-based metabolic network analyses, several specialized software tools are required. In this section, we will install and configure two key components: the COBRA Toolbox and Gurobi. The COBRA Toolbox is a MATLAB-based software suite specifically designed for the analysis of genome-scale biochemical networks, while Gurobi is a state-of-the-art optimization solver that provides a MATLAB interface for executing linear and mixed-integer linear programming tasks.

The Constraint-Based Reconstruction and Analysis (COBRA) Toolbox is widely recognized for its robust framework, enabling quantitative predictions of cellular and multicellular biochemical networks under various constraints. It implements an extensive range of methodologies, from fundamental reconstruction and model generation techniques to advanced, unbiased approaches for model-driven analysis. By integrating the COBRA Toolbox into a MATLAB environment, researchers gain access to a versatile platform for modeling, analyzing, and predicting diverse metabolic phenotypes at the genome scale [Heirendt et al., 2019].

Gurobi is a state-of-the-art mathematical optimization solver, widely recognized for its exceptional performance and reliability in solving a broad spectrum of linear, integer, and mixed-integer linear programming problems. Its advanced algorithms, parallelized computations, and extensive parameter tuning options make it one of the most efficient and user-friendly optimization tools available. [Gurobi 12.0 Documentation, 2024] By providing a robust MATLAB interface, Gurobi seamlessly integrates with the COBRA Toolbox and other computational frameworks, thereby streamlining model-driven analysis and facilitating rapid, large-scale solution of complex optimization problems.

DFBAlab, a MATLAB-based simulator that uses the LP feasibility problem to obtain an extended system and lexicographic optimization to yield unique exchange fluxes, is presented. DFBAlab is able to simulate complex dynamic cultures with multiple species rapidly and reliably, including differential-algebraic equation (DAE) systems [Gomez et al., 2014]. DFBAlab can be obtained by visiting the official website, which is provided by the Process Systems Engineering Laboratory (PSEL) at MIT.

Tip

In MATLAB, you can permanently add a folder to your search path (so MATLAB can always find the functions in that folder) by following these steps:

1. On the Home tab, in the Environment section, click Set Path.

2. In the Set Path dialog, click Add Folder. Select the folder containing your functions, then click Open. Finally, click Save.

A CSTR Model for Microbial Growth

In a continuous stirred-tank reactor (CSTR) designed for a yeast microbial fermentation, as shown in Fig. 6, four extracellular components are typically tracked: biomass, glucose, oxygen, and ethanol. The reactor is operated at a constant volume with a continuous feed of nutrients (media) that supports cell growth. Below is a concise overview of the main material balances, highlighting how each component is added, consumed, or removed from the system.

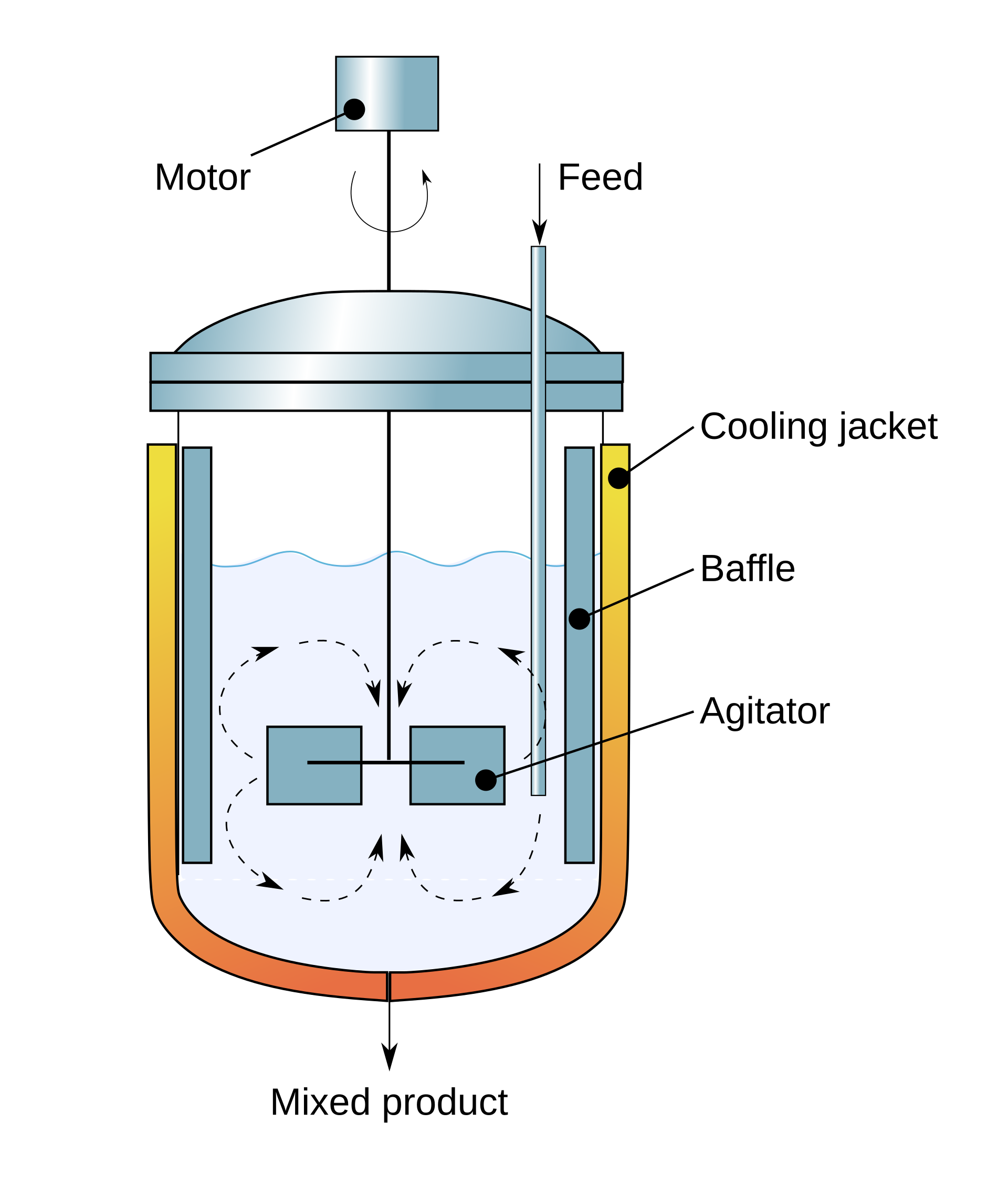
Fig. 6 Cross-sectional diagram showing the setup of a continuous stirred-tank reactor

1. Biomass Balance

Governing Equation:

(6)\[\frac{d[X]}{dt} = 0 - v_{1} - D X + \mu X\]

where:

• \(X\) is the biomass concentration \([g/L]\).

• \(D\) is the dilution rate \([h^{-1}]\), defined as the volumetric feed flow rate divided by the reactor volume.

• \(\mu\) is the specific growth rate \([h^{-1}]\), obtained from the metabolic model or flux balance analysis.

In this balance, there is no inflow of cells (i.e., feed does not contain biomass), so the only sources and sinks are (a) the growth of biomass within the reactor and (b) the washout of cells at the outflow. The accumulation term is therefore governed by the net of growth minus outflow.

2. Glucose Balance

Governing Equation:

(7)\[\frac{d[G]}{dt} = D (G_{f} - G) - v_{G} X\]

where:

• \(G\) is the glucose concentration in the reactor \([mM]\) or \([g/L]\).

• \(G_{f}\) is the feed (inlet) glucose concentration.

• \(v_{G}\) is the specific uptake rate of glucose \([mMg^{-1} h^{-1}]\), which can also be predicted by the metabolic model.

3. Ethanol Balance

Rather than being consumed like glucose, sucrose, and fructose, ethanol is produced by the cells during the process of fermentation. Hence, in a typical CSTR:

(8)\[\frac{d[E]}{dt} = D (E_{f} - E) + v_{E} X\]

where:

• \(E\) is the ethanol concentration in the reactor.

• \(E_{f}\) is the feed ethanol concentration (commonly zero if ethanol is not fed).

• \(v_{E}\) is the specific production rate of ethanol determined by the metabolic model.

Because ethanol is formed as a metabolic by-product, \(v_E\) is typically a positive term, signifying net production.

4. Oxygen Balance

Oxygen transfer in a CSTR is more complex, as oxygen is often supplied via sparging or agitation to promote gas–liquid mass transfer. The basic form of the oxygen balance can still be written similarly:

(9)\[\frac{d[O]}{dt} = D (O_{f} - O) + k_{L}a (O_{gas} - O) - v_{O} X\]

where:

• \(O\) is the dissolved oxygen concentration in the liquid phase.

• \(O_{f}\) is the feed concentration of dissolved oxygen (which may be zero if the feed is not pre-saturated).

• \(k_{L}a\) is the volumetric mass transfer coefficient, and \((O_{gas} - O)\) represents the driving force for oxygen transfer from the gas phase into the liquid.

• \(v_O\) is the specific consumption rate of oxygen by the cells.

In practice, the oxygen concentration depends on both the rate of cellular consumption and the efficiency of mass transfer. Thus, for highly active cultures, oxygen can become rate-limiting if it is not supplied at a sufficiently high transfer rate.

Example: DFBA with iND750 Yeast Model

You are given the iND750 genome-scale metabolic model for S. cerevisiae. In a laboratory setting, you want to grow this yeast under the following conditions:

• Carbon Source (Glucose): 20 g/L

• Oxygen (Gas): 2 mmol/L

• Time Span: 100 hours

Use Dynamic Flux Balance Analysis (DFBA) to determine the carbon consumption and yeast’s predicted biomass concentration (or specific growth rate) profiles under these constraints.